Warnock Subdivision for Deferred Lighting June 12th, 2015
I wanna talk about Warnock's Algorithm today. Despite something that used to be fairly well-known, it seems to have fallen by the wayside a little nowadays. The algorithm was first described in 1969 by John Warnock. (In case you haven't heard of him, he went on to start a small graphics company called Adobe).
The algorithm originally was designed for hidden-surface removal, which at the time was a big problem. Nowadays people tend to just use Z-buffers, and while that's probably a good thing in terms of the original application, sometimes old things can be repurposed for newer problems.
It turns out the actual algorithm itself is much more interesting than simply sorting polygons - it's a general-purpose technique for any situation where you have lots of 2D things and you want to either group or simplify them for processing.
So in order to demonstrate the algorithm, let's pick a more modern use-case to look at.
Deferred Lighting
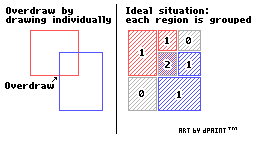
If you're writing a deferred renderer, you get to a point where you need to draw your lights on-screen. Let's assume we've already worked out the 2D screen bounding box of each light. All we need to do then is draw a quad which will then rasterize the light into the lighting buffer.
However, there's a problem here. Each light has a certain amount of overhead - your shader has to read the Z-buffer value and reconstruct the 3D position. Then once you've done the actual lighting, you need to write and blend the color onto the lighting framebuffer.
All this overhead adds up, so what you really want to do is find a way to get a list of the lights that overlap on-screen, and group those together into batches. That way you only need to read the Z-buffer and reconstruct the position once for each screen pixel, and then share that cost across multiple lighting calculations.
One way to do this is described by Naughty Dog, as part of their PS3 Uncharted engine. They split the screen into fixed-size tiles, and for each light they work out which tiles it overlaps. Each tile gets a list of all the lights that affect it, and can then process many of them at a time.
Now to be honest, that's a pretty reasonable way to do it. It does have the disadvantage that you end up lighting more pixels than necessary, because your light will probably fall somewhere that isn't aligned to tile boundaries. So you light a few more pixels than necessary.
Warnock subdivision can instead get a pixel-accurate list of the lights needed at any point. Depending on how many lights you have, and how big they are on-screen, one approach may be better than the other. You may find the Naughty Dog method works better for your game. Or perhaps the other way around. You could even find it's better to not use rectangles for your lights.
I'm not claiming subdivision is the absolute best way to solve this problem for all use-cases.
But wouldn't the world be a terribly boring place if there was only one way to do everything?
Warnock Subdivision
To explain the motivation I'll quote from Warnock's original paper, because it's really quite interesting:
Warnock, 1969 - A hidden surface algorithm for computer-generated halftone pictures
The description of the philosophy is best given by describing the motivation behind it. Suppose I examine a picture of a table with pencils on it. I quickly determine that large areas on top of the table are open and therefore have little information content.
I scan over these areas searching out complex features such as a pencil. I dwell on a complex portion until I assimilate the information associated with it. From there I scan to other areas of the picture looking for additional complexity. In scanning the picture in this way I seem to spend little or no time on simple areas.
Complex areas seem to present themselves to me as subproblems requiring a solution. I seem to reduce these problems into further subproblems until I either solve the subproblem or don't care anymore.

The 3 categories we need to consider.
The idea of Warnock's algorithm is, given a 2D rectangular window, and a list of things, to classify each thing into one of three categories:
- Things entirely outside the window.
- Things that are simple enough to deal with right here.
- Things that are complex enough that we can't deal with them yet.
The things outside the window are obviously the easiest to handle - we just ignore them. For things that are simple, the exact meaning of "simple" depends on your particular application. In the original application (polygon rendering), simple meant "this polygon covers the entire window". So in that case you could just fill the whole window with that polygon's color.
The third case is the trickiest. The way Warnock's algorithm deals with complex things is to recurse - we throw out the things outside the window, and try again with a smaller window. Eventually we're guaranteed to get down to the level of a single pixel, at which point everything will fall into case 1 or 2 anyway.
Grouping Lights
So how do we apply this to deferred lighting? What we want is to split the screen into regions, where each region is assigned a list of lights that need to be rendered there. Once we have that list, we can render each region as a batch.
To get optimal results, we want to make sure that each output region does not have any light-edges within it. i.e. All lights in a region must fully cover that region.
So here's the three classifications we need:
- The light's rectangle is entirely outside the current window. (ignore)
- The light's rectangle fully covers the current window. (simple)
- The light's rectangle partially covers the current window. (complex)
We process each incoming rectangle in turn, and classify it into one of those three categories. After we're done, we see if there are any partially-overlapping lights. If there are, we need to recurse with four smaller windows, and a smaller list that has the "outside" items removed. Otherwise, we now have a 2D window on screen and a list of all the lights that are relevant for that window, and we can do the rendering right there.
The only remaining question is when we recurse with a smaller window, how do we know where to split the window at? One option is to split the window exactly in half. This works fine, but isn't optimal. We can do better by using one of the light's edges to split along. So as we perform our classification, we keep an eye out for possible good edges to use later.
A note on storage
This algorithm runs entirely in-place on the list that's passed in. There's no need to call new or delete during the operation of it, which makes it very fast.
Although we need to track 3 different lists as we classify each rectangle, we don't need to allocate any new lists. We can simple re-use the original storage, and swap items around within that storage. We track where the start and end of each list are as we classify them.
In his classic book "Dirty Pixels", Jim Blinn refers to this technique as being a "triage table", and describes how it can be used for many kinds of recursive algorithms. It's well worth a read if you're at all interested in graphics algorithms. (in fact, Blinn uses Warnock subdivision as a prime example, which is where I first read about it).
This does mean that the source list of rectangles gets rearranged during the course of the algorithm. This isn't usually a problem as the list gets regenerated every frame by the game anyway.
Demo
There should be an interactive demo here. If you can't see it... uh.. sorry. Browsers and all that.
Draw new rectangles out with the mouse. Hover over 2D regions to see which rectangles are needed for that region.
Source code
You can download the entire C++ source code for the above demo here. If you find it useful, please let me know!
- Complete demo source code (C++/SDL)
I've listed the relevant core function below as well.
// Renders a set of overlapping rectangles on-screen by
// recursively subdividing them into regions where
// each region contains no rectangle edges.
void warnockSubdivide(Rectangle *list, int count)
{
// Initialize the stack to the whole window, and all the rectangles.
int stackSize = 1;
State stack[MAX_RECTANGLES*4];
stack[0] = (State) { list, count, 0, 0, screen->w, screen->h };
while (stackSize > 0)
{
// Pop a new window off the stack.
State s = stack[--stackSize];
// Check if our current window is OK to render to:
if (s.x1 <= s.x0 || s.y1 <= s.y0)
continue;
// If we need to recurse, we'll need to decide on a point
// within the window to split at. We really want it to be
// on the edge of a rectangle. We'll fill it in blank for
// now and get a better guess as we test each rectangle.
int splitX = s.x0, splitY = s.y0;
// Let's treat our list of rectangles as a "triage table".
// This means we consider the list as 3 categories:
//
// |---outside---|---partial---|---remaining---|---inside---|
// ^- read cursor
//
// The 'remaining' list initially contains every item, with
// the other lists being empty.
// We process through the 'remaining' list, and move each item
// into its appropriate category. We can do this entirely
// in-place within this one array.
// Once the 'remaining' list is empty (i.e. the read cursor
// is equal to the start of the 'inside' list) then we're done.
int endOutside = 0; // index of the end of the 'outside' list.
int startInside = s.count; // index of the start of the 'inside' list.
// Classify each rectangle into one of three categories:
// a) The rectangle is entirely outside our window
// b) The rectangle entirely covers our window
// c) The rectangle partially intersects our window
for (int n=0;n<startInside;)
{
const Rectangle &r = s.list[n];
// Compute the in/out clipping codes.
// A code has one of four bits set depending
// on whether that edge intersects our window.
int outcode = 0, incode = 0;
if (r.x0 >= s.x1) outcode |= 1;
if (r.y0 >= s.y1) outcode |= 2;
if (r.x1 <= s.x0) outcode |= 4;
if (r.y1 <= s.y0) outcode |= 8;
if (r.x0 <= s.x0) incode |= 1;
if (r.y0 <= s.y0) incode |= 2;
if (r.x1 >= s.x1) incode |= 4;
if (r.y1 >= s.y1) incode |= 8;
if (outcode != 0) {
// Rectangle is entirely outside this window.
// Move it to the 'outside' list.
std::swap(s.list[n++], s.list[endOutside++]);
} else if (incode == 0xf) {
// Rectangle entirely covers this window.
// Move it to the 'inside' list.
std::swap(s.list[n], s.list[--startInside]);
} else {
// This rectangle partially covers, so we'll
// see if one of its edges can be used as a suitable
// split point in case we need to recurse later.
// Another option is to simply split the window exactly
// in half - this is easier to do, but generates more
// output regions than necessary.
if (!( incode & 1))
splitX = r.x0;
if (!( incode & 2))
splitY = r.y0;
if (!( incode & 4))
splitX = r.x1;
if (!( incode & 8))
splitY = r.y1;
// Leave this rectangle where it is and
// grow the 'partial' list to cover it.
n++;
}
}
// Throw away the ones that are entirely outside, giving
// us a list of ones that are either entirely or partially
// within our window.
int numChild = s.count - endOutside;
Rectangle *children = s.list + endOutside;
// If we have any partials, we recurse with smaller windows.
int numPartial = startInside - endOutside;
if (numPartial > 0)
{
stack[stackSize++] = (State){ children, numChild, s.x0, s.y0, splitX, splitY };
stack[stackSize++] = (State){ children, numChild, splitX, s.y0, s.x1, splitY };
stack[stackSize++] = (State){ children, numChild, s.x0, splitY, splitX, s.y1 };
stack[stackSize++] = (State){ children, numChild, splitX, splitY, s.x1, s.y1 };
} else {
// Otherwise we now know that everything in this list
// entirely covers our window, so we can just stop here and draw them all.
State final = { children, numChild, s.x0, s.y0, s.x1, s.y1 };
drawRectangleList(final);
}
}
}
Written by Richard Mitton,
software engineer and travelling wizard.
Follow me on twitter: http://twitter.com/grumpygiant
